| | dr. Dejan Dragan1 | | dr. Tomaž Kramberger1 | | dr. Klemen Prah1 | | Marko Intihar1 | | 1 Fakulteta za logistiko Univerze v Mariboru | |
|
| Povzetek V prispevku je predstavljen dvokoračni optimizacijski postopek za potrebe krčenja stroškov prevoza določenih kategorij otrok v šolo v občini Laško. Na osnovi zakonskih predpisov jih je potrebno vsak dan razvoziti na pripadajoče šole ter jim zagotoviti tudi vrnitev domov. V prvem koraku postopka, ki temelji na uporabi simulacije Monte Carlo, je najprej treba določiti lokacije optimalnih postaj, s katerih naj bi vozila pobirala in odlagala učence. Pri tem je bil za zbiranje podatkov uporabljen geografski informacijski sistem (GIS). Kot se izkaže, je algoritem zmožen izračunati najmanjše možno število postaj, ki pa bodo vseeno zagotavljale največje možno pokritje učencev v okviru predpisanega največjega radija pešačenja. Prav tako bo pri izračunanih optimalnih postajah potrebno učencem prehoditi najkrajšo možno pot od doma do najbližje postaje in obratno. V drugem koraku optimizacijskega postopka je potrebno glede na izračunane optimalne lokacije postaj iz prvega koraka izvesti še optimizacijo voznih poti in voznih redov prevoznih sredstev. V ta namen je bila izbrana računalniška programska oprema, ki temelji na uporabi programov ESRI ArcLogistics 9.3 in ESRI ArcView 9.31. V prispevku so opisane glavne značilnosti delovanja mehanizma predlaganega dvokoračnega algoritma. Opisana je tudi metodologija za pripravo programske opreme za optimizacijo voznih poti in voznih redov. Prav tako je podan prikaz vseh pomembnih izračunanih rezultatov. Pozicije izračunanih optimalnih postaj, optimalne poti in optimalni vozni redi se bodo uporabili pri dejanskem načrtovanju in instalaciji z namenom kar največjega možnega zmanjšanja transportnih stroškov. Ključne besede: lokacijski problemi, optimizacija, simulacija Monte Carlo, geografski informacijski sistem (GIS), programski orodji ArcLogistics in ArcView. |
|
Verzijo za tisk si lahko prenesete  tukaj (pdf).
tukaj (pdf).
1 Uvod
Prispevek obravnava problematiko krčenja specifičnih kategorij stroškov, do katerih prihaja v občini Laško, kjer je potrebno na osnovi zakonskih predpisov zagotoviti prevoz določenih kategorij otrok v pripadajoče šole ter zagotoviti njihovo vrnitev domov.
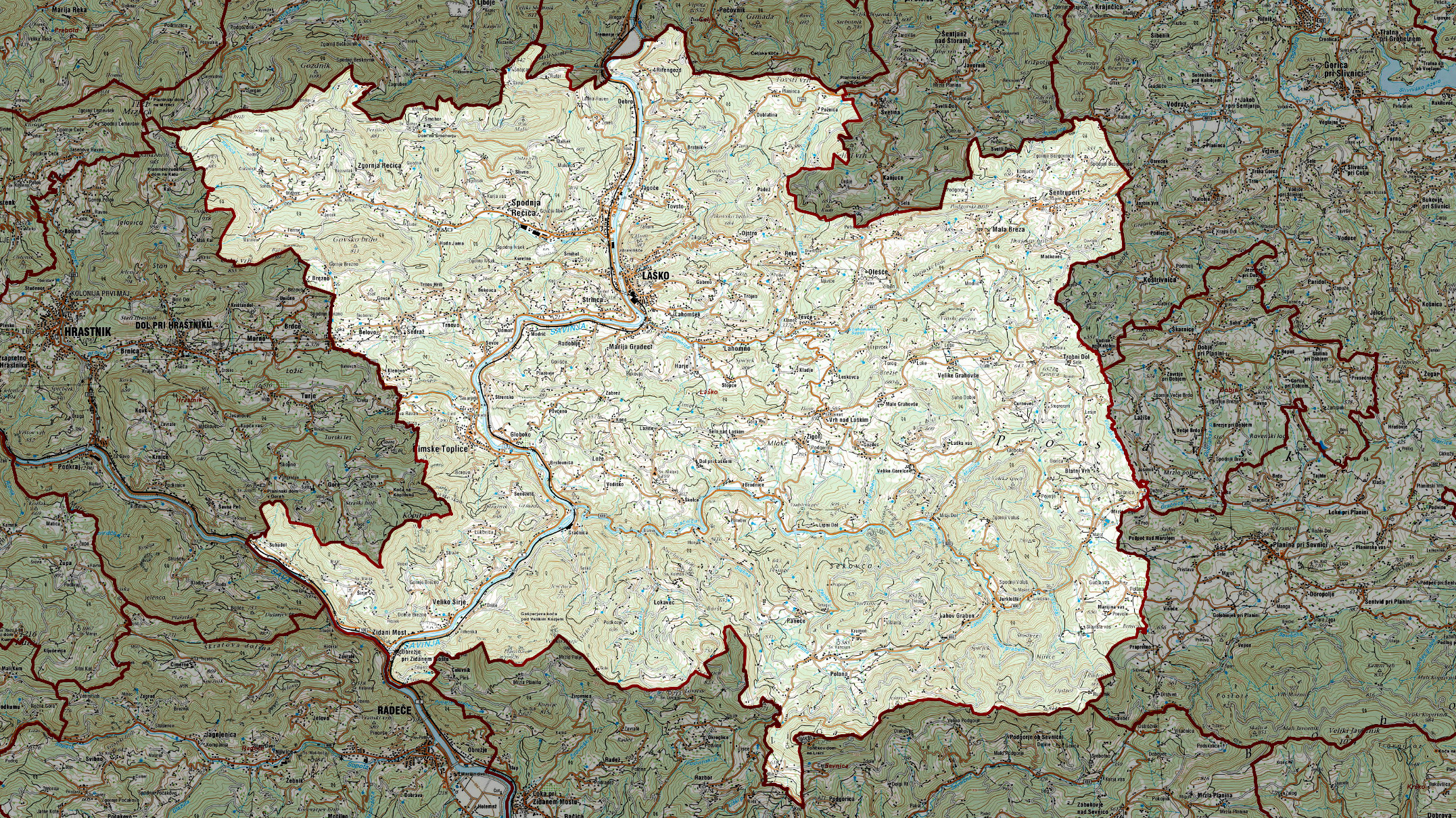
Slika 1 prikazuje pozicije naslovov učencev v občini Laško (osenčeno področje). V danem trenutku je obravnavanih 562 učencev, ki so označeni s krogci na sliki 1. Slika 1 prikazuje tudi pozicije šol (hiške), katerih skupno število je 11.
Ker so v današnjem času omenjeni transportni stroški postali nevzdržni, jih je vsekakor potrebno kar najbolj skrčiti. Glavni razlog za tako visoke stroške je trenutna neustrezna organizacija transporta. Pri prevozu otrok v šolo se dogaja, da avtobusi in ostala prevozna sredstva, ki jih je najela občina, pobirajo slehernega učenca prav na hišnem pragu, prav tako ga tudi dostavijo neposredno domov. Poleg tega so transportne poti dokaj neorganizirane v smislu nepotrebnih dodatno prevoženih kilometrov, vozila so pogostokrat napol prazna, posamezne vozne poti se večkrat po nepotrebnem podvajajo itn.
Zmanjševanje omenjenih kategorij stroškov je mogoče doseči z uporabo dvokoračnega optimizacijskega pristopa, prikazanega na sliki 2 (Dragan in Kramberger, 2009). V prvem koraku tega postopka je najprej potrebno določiti in implementirati lokacije optimalnih postaj, s katerih naj bi vozila pobirala učence v prihodnosti. To bi seveda pripomoglo k nastanku dveh posledic. Po eni strani bi bili učenci prisiljeni hoditi od njihovih domov do najbližjih postaj in bi izgubili privilegij, da bi se jih pobiralo na domu. Vendar pa bi bilo potrebno po drugi strani transportnim sredstvom prevoziti bistveno manj poti, če bi morala pobirati učence le na postajah, ne pa prav vsakega neposredno na njegovem domu.
Seveda potrebnega števila in lokacij postaj ni priporočljivo določiti kar naključno kjerkoli na obravnavanem območju, pač pa mora biti tovrstno načrtovanje zelo skrbno. Glavno vodilo pri tem je, da naj bi bilo postaj čim manj, sleherna od njih pa naj bi pokrivala kar največje možno število učencev, seveda pri upoštevanju predpisanih omejitev pešačenja, v okviru katerih bi bilo potrebno učencem prepešačiti kar najkrajšo možno pot.
Za potrebe doseganja teh ciljev je bila pri izračunu optimalnih postaj uporabljena kombinirana simulacijsko-optimizacijska procedura, ki temelji na simulaciji Monte Carlo (Dragan in Kramberger, 2009) in se nekoliko razlikuje od klasičnih pristopov k reševanju lokacijskih problemov.
V drugem koraku optimizacijskega postopka na sliki 2 je potrebno glede na izračunane optimalne lokacije postaj iz prvega koraka izvesti še optimizacijo voznih poti in voznih redov prevoznih sredstev. V ta namen je bila izbrana računalniška programska oprema, ki temelji na uporabi programov ESRI ArcLogistics 9.3 in ESRI ArcView 9.31.
S pomočjo programa ArcView in njegove ekstenzije Network Analyst je bila najprej pripravljena kartografska podlaga občine Laško, kjer so bili ustrezno zajeti in obdelani vsi potrebni podatkovni sloji. Ko so bili vnešeni še podatki o vseh lokacijah, vozilih in naročilih ter je bila potemtakem programska oprema za optimizacijo voznih poti in voznih redov v celoti pripravljena, je bilo moč izvesti postopek optimiranja s pomočjo programa ArcLogistics.
Doseženi rezultati za izračunane optimalne postaje, vozne poti in vozne rede kažejo, da bi se dalo z implementacijo teh rezultatov doseči občutne prihranke pri dnevni kilometrini obravnavanih vozil, kar pa bi posledično vodilo tudi k občutnemu zmanjšanju obstoječih stroškov.
2 Definicija problema in začetna redukcija cestnih podatkov
Na sliki 3 so prikazane lege vseh 14.295 točk obstoječih cest (kvadratki) v občini Laško, ki so hkrati tudi možni kandidati za postaje (KZP). Dotične točke so bile generirane s pomočjo 300-metrske segmentacije vsake posamezne ceste znotraj obravnavanega področja. Segmentirane točke cest so bile zbrane na osnovi podatkov iz geografskega informacijskega sistema (GIS) (Harmon in Anderson, 2003). Pozicije naslovov 562 učencev (NU) so označene s krogci na sliki 3 in so bile prav tako zbrane s pomočjo GIS.
Porazdelitev točk učencev se obravnava na površini 247,9 km2(označeno področje A na sliki 3), medtem ko so točke cest razpršene na mnogo večjem področju (več kot 300 km2). Ker je možnih kandidatov (točk cest) za postavitev postaj silno veliko in so postaje razpršene na ogromni površini, je najprej potrebno izvesti začetno redukcijo cestnih podatkov. Pri tem se uporabi določena hevristična pravila (Dragan in Kramberger, 2009), s katerimi uspemo začetno število 14.295 možnih točk cest zreducirati na bolj sprejemljivo število 1.768 kandidatov.
Ker pa je to število še vedno preveliko s stališča stroškov postavitve postaj, je v nadaljevanju potrebno izvesti še dodatno redukcijo cestnih podatkov s pomočjo optimizacije na osnovi simulacije Monte Carlo, ki nam kot rezultat izračuna optimalne postaje (1. korak na sliki 2).
3 Določitev optimalnih postaj s pomočjo optimizacije na osnovi simulacije Monte Carlo
Mehanizem delovanja postopka optimizacije na osnovi simulacije Monte Carlo je natančno razložen v dveh prispevkih (Dragan in Kramberger, 2009). V tem postopku je najprej potrebno opazovano področje s 1.768 kandidati za postaje razdeliti na določeno število podsektorjev. Vsak izmed njih pokriva določeno število kandidatov za postaje in določeno število naslovov učencev. Nato je potrebno za vsak podsektor ugotoviti, kateri kandidati za postaje zagotavljajo najbolj učinkovit servis največjemu možnemu številu učencev. To pomeni, da pokrijejo znotraj krogov s predpisanim radijem r največ učencev v dotičnem podsektorju, pri čemer je skupna razdalja pešačenja “pokritih” (razporejenih) učencev do najbližjih postaj najkrajša možna. Dodatni kriterij je, da je število “nepokritih” (nerazporejenih) naslovov učencev, ki morajo hoditi dlje od predpisanega radija do katerekoli postaje, kar najmanjše možno.
Kot se izkaže, je možno ta problem učinkovito rešiti z uporabo procedure Monte Carlo. V okviru izvajanja simulacij te procedure se vsakič generira za vsak podsektor set naključno izbranih točk cest, ki jih obkrožimo s krogi predpisanega radija. Za te točke se v vsaki simulaciji tudi izmerijo razdalje do pokritih učencev znotraj krogov ter se prešteje število nepokritih učencev. Ko je postopek izvajanja simulacij končan, se poskuša določiti za vsak podsektor najbolj ugoden set naključno izbranih točk cest. To je tisti set, pri katerem je vsota razdalj med točkami cest posameznega seta in točkami pokritih učencev najmanjša možna ter je hkrati najmanjše možno število nepokritih učencev.
Kombinacija izračunanih rezultatov za vse podsektorje, kar pomeni “najboljše” sete naključno izbranih cestnih podatkov za vsak podsektor, predstavlja pozicije optimalnih postaj. Pri tem konceptu lahko govorimo o naslednji predpostavki. Če so optimalne postaje izračunane na takšen način, je število izračunanih lokacij postaj najmanjše možno, te pa pokrivajo največje možno število učencev znotraj predpisanega radija. Pri tem je učencem v povprečju potrebno prehoditi najkrajše možne razdalje do postaj, hkrati pa je tudi število nerazporejenih učencev najmanjše možno.
Ko se je optimizacijska procedura na osnovi simulacij Monte Carlo izvršila, so se izračunale (X,Y) koordinate 48 optimalnih postaj. Kot se izkaže, so optimalne postaje zmožne pokritja 554 učencev znotraj predpisanega radija 1,4 km, kar predstavlja 98,5-odstotno pokritost celotnega števila 562 učencev. Pri tem bi 8 učencev ostalo nerazporejenih, vendar tudi tem ne bi bilo potrebno hoditi dlje kot nekaj 100 m več od predpisanega radija.
Na sliki 4 je predstavljena prostorska porazdelitev izračunanih 48 optimalnih postaj (znaki za male “avtobuse”). Njihove koordinate so že bile izročene pristojnemu osebju v občini Laško, da bi se lahko začelo izvajati njihovo fizično implementacijo. Ko bodo te instalacije končane, bodo morali vozniki transportnih sredstev pobirati učence le na 48 optimalnih postajah, namesto da bi morali vsakega izmed 562 učencev posebej pobirati na domu. Očitno bo že z uvedbo postaj ustvarjen precejšen prihranek pri transportnih stroških.
4 Optimizacija poti in voznih redov
Ko so izračunane optimalne lokacije postaj iz prvega koraka procedure na sliki 2, je potrebno izvesti še optimizacijo voznih poti in voznih redov prevoznih sredstev (2. korak na sliki 2). V ta namen je bila izbrana računalniška programska oprema, ki temelji na uporabi programov ESRI ArcLogistics 9.3 in ESRI ArcView 9.31 (Terrey, 2008).
Da bi se lahko omenjena programska oprema učinkovito uporabila pri tovrstni optimizaciji, je seveda potrebno izvesti tudi vse nastavitve in vnesti vse podatke. Kar se slednjih tiče, je potrebno poleg izračunanih optimalnih lokacij postaj, od koder naj bi vozila pobirala otroke, definirati tudi pozicije njihovih šol ter nabor in izhodiščne pozicije vozil razpoložljivega voznega parka (glej sliko 4). Kot je razvidno iz slike 4, imamo opravka z 11 šolami ter 5 izhodiščnimi lokacijami prevoznih sredstev.
Za izhodiščne lokacije vozil velja, da v njih vozila, ki prevažajo otroke, bodisi začnejo bodisi končajo svojo pot. Pri tem je trenutni vozni park sestavljen iz naslednjih vozil:
- 3 avtobusi s kapaciteto 50 potnikov,
- 1 minibus s kapaciteto 16 potnikov ter
- 10 kombijev s kapaciteto 8 potnikov.
Poleg vseh potrebnih podatkov o lokacijah (postaje, vozila, šole) je potrebno opraviti tudi ustrezne nastavitve programske opreme, ki bi jih lahko razdelili v naslednje smiselne sklope:
- osnovne nastavitve programske opreme, zlasti za cestno omrežje,
- nastavitve programske opreme za potrebe razvoza učencev od optimalnih postaj do šol (pot v šolo),
- nastavitve programske opreme za potrebe razvoza učencev od šol do optimalnih postaj (pot iz šole).
Kar se tiče osnovnih nastavitev cestnega omrežja, je bila s pomočjo programa ArcView pripravljena kartografska podlaga občine Laško, kjer so bili zajeti naslednji štirje podatkovni sloji:
- meja občine Laško,
- cestna mreža,
- osnovne šole in
- predlaganih 48 optimalnih postajališč.
Podatkovni sloji so izdelani v Gauss-Krügerjevem projekcijskem koordinatnem sistemu. Pri tem vire za podatkovne sloje meje občine, cestne mreže in osnovnih šol predstavljajo podatki podjetja NAVTEQ s sedežem v ZDA. Tako je bila npr. meja občine Laško pridobljena iz sloja Adminbndy4, cestna mreža iz sloja Streets, osnovne šole pa so bile dobljene iz sloja PointAddress.
Za potrebe učinkovite uporabe programa za optimizacijo (poti in voznih redov) ArcLogistics je bilo potrebno tudi ustrezno obdelati podatkovni sloj o cestni mreži s pomočjo Network Analysta, ki predstavlja ekstenzijo programa ArcView. Pri tem je bil izdelan tako imenovan Network Dataset, sestoječ iz linijskega sloja cestnih odsekov in točkovnega sloja vozlišč (Junctions), ki med seboj povezujejo cestne odseke. Pomembno je namreč, da je sloj cestnih odsekov opremljen z atributom trajanja vožnje na posameznem odseku (v minutah), z morebitnimi prepovedmi za določena vozila (atribut RESTRICTION), podvozi in nadvozi (pridobljeno iz podatkovnega sloja Zlevels).
V kompaktni obliki torej naštejmo nekaj bistvenih nastavitev za cestno omrežje, ki smo jih uvedli pri osnovnem nastavljanju Network Dataseta:
- nastavitve glede hitrostnih omejitev, ki veljajo pri posameznih cestah,
- nastavitve nivojev cest (podvozi, nadvozi itn.) ter
- nastavitev kategorizacije cest (enosmerne ceste, dvosmerne ceste itn.).
Poleg vnosa lokacij in osnovne priprave cestnega omrežja je potrebno za potrebe programa ArcLogistics izvesti tudi nastavitve, ki se neposredno tičejo razvoza otrok od optimalnih postaj (kamor so prišli od svojih domov), pa do njihovih šol ter razvoza v obratni smeri (torej od šol nazaj do postaje, od koder se vrnejo domov).
Pri teh nastavitvah je potrebno upoštevati naslednje pomembne dejavnike za vozila (smer postaje–šole):
- določitev časa začetka pobiranja otrok na optimalnih postajah (izbran je bil čas 6.20);
- določitev časa, do katerega naj bi bili vsi otroci razvoženi od postaj do šole (izbran je bil čas 8.00);
- določitev časa, potrebnega za vkrcanje in izkrcanje enega učenca v posamezno vozilo ali iz njega (izbran je bil čas 8 sekund – 0,133 minute); seveda se ta čas sešteva, če vozilo pobere na postaji več učencev naenkrat;
- določitev stroškov prevoznih sredstev na podlagi trenutnih pogodbenih cen prevoza, ki so podani v tabeli 1.
Kar se tiče nastavitev za obratno smer prevoza (šole–postaje), je potrebno upoštevati naslednje pomembne dejavnike za vozila:
- določitev časa začetka pobiranja otrok na šolah, ko zaključijo pouk (izbran je bil čas 13.00);
- čas vkrcanja ali izkrcanja posameznega učenca v vozilo ali iz njega je bil izbran enak kot v smeri prevoza: postaje–šole (torej 8 sekund);
- glede časa, do katerega naj bi bili vsi otroci razvoženi iz šol nazaj na postaje, naročnik ni imel posebnih zahtev.
Pri obratnem razvozu (šole–postaje) je pomembno še poudariti, da so določene dodatne nastavitve, ki smo jih izvedli tu, odvisne od kasnejšega postopka optimizacije, ki ga ArcLogistics izvede za potrebe razvoza otrok od optimalnih postaj do pripadajočih šol. Med izvajanjem postopka namreč program tudi določi, katera vozila naj poberejo katere skupine otrok in na katerih postajah. Tako program dodeli točno določene skupine otrok točno določenim vozilom. Ideja je, da bi pri obratnem transportu, torej od šol do postaj, dodelili iste skupine otrok istim vozilom, ki so jih že zjutraj razvozila od postaj do šol.
Ko so vse nastavitve, parametri in podatki ustrezno vnešeni in torej dostopni programu ArcLogistics, se lahko slednjega požene za izvedbo optimizacijskega postopka. Pri tem postopku se izvede optimizacija voznih poti in voznih redov razpoložljivih vozil.
V ozadju optimizacije se seveda izvaja minimizacija določene stroškovne funkcije, pogojene s stroški, ki nastanejo pri različnih kombinacijah scenarijev prevoza otrok glede na različne poti, razporeditev in obremenitev voznega parka itn.
Seveda je najbolj ugodna tista rešitev optimizacije, poganjana z ustreznimi hevrističnimi optimizacijskimi postopki (Prasertsri in Kilmer, 2003), pri kateri je dosežen optimalen kompromis naslednjih dejavnikov:
- stroškovna funkcija je najmanjša možna,
- skupno število prevoženih kilometrov naj bo karseda minimalno,
- vozila naj bodo čim bolj napolnjena z učenci,
- podvajanj poti naj bo čim manj.
5 Praktični numerični rezultati optimizacije voznih poti in voznih redov (smer postaje–šole)
Rezultate izračunanih optimalnih poti vseh 14 vozil lahko za smer (postaje–šole) kompaktno strnemo na slikah 5 in 6. Seveda je ArcLogistics za vsako izmed teh optimalnih poti izračunal tudi optimalne vozne rede, ki se jih morajo vozniki vozil dosledno držati, če želimo res prispevati k čim večji redukciji obstoječih stroškov prevoza otrok.
Vsako izmed vozil na slikah 5 in 6 pri izvajanju optimalnih poti vsebuje svojo izhodiščno lokacijo, določen nabor optimalnih postaj, ki jih mora “obdelati” oz. na njih pobrati otroke, ter določen nabor šol, kamor mora te otroke razvoziti. Tabela 2 natančno prikazuje te atribute, torej katere optimalne postaje in šole se na osnovi optimizacije dodeli posameznim vozilom.
Kot se izkaže, veljajo za obratno pot razvoza (šole–postaje) dokaj podobne, vendar ne identično enake optimalne poti, kot so prikazane za smer (postaje–šole) na slikah 5 in 6. Ta podobnost je tudi razumljiva, saj smo pri nastavitvah programske opreme določili, da morajo ista vozila na šolah pri obratnem transportu pobirati iste skupine otrok, ki so jih pripeljale do teh šol, ter jih razvoziti nazaj na iste optimalne postaje.
Poglejmo si še primer določenega segmenta optimiranega voznega reda enega izmed vozil, konkretno gre za vozilo kombi 2. Slika 7 prikazuje primer strukture optimalnega voznega reda za kombi 2, ki vsebuje natančne usmeritve za voznika. Te usmeritve se tičejo tako vrstnega reda premikov kombija, ki se jih mora voznik držati, kot tudi vrstnega reda skupin učencev, ki jih mora spotoma na optimalni poti pobirati. Podane so seveda tudi informacije, na katerih optimalnih postajah mora določene skupine učencev pobrati ter šol, kamor jih mora razvoziti.
Podobna struktura optimalnih voznih redov, kot je prikazana na sliki 7 za kombi 2, je bila pri optimizaciji z ArcLogisticsom izdelana tudi za voznike vseh ostalih vozil, tako pri izvajanju optimalne poti na relaciji od postaj do šol kot tudi v obratni smeri.
6 Analiza prevoženih kilometrov pri optimalnih poteh in voznih redih (obe smeri transporta)
Tabela 3 prikazuje skupno dnevno kilometrino in skupne stroške prevoza za obe smeri transporta (postaje–šole, šole–postaje) pri optimalnih poteh in optimalnih voznih redih vozil. Kot je razvidno iz tabele 3, bi vozila pri obeh smereh transporta po optimalnih potih vsak dan prevozila v skupnem seštevku okrog 2.091 kilometrov, pri čemer bi nastalo za okrog 1.873 evrov skupnih stroškov prevoza otrok.
Kot se izkaže na osnovi primerjave skupne dnevne kilometrine 2091,1 km v primeru optimalnih poti in voznih redov (tabela 3) z obstoječim (neoptimalnim) stanjem (več kot 3.000 km na dan), očitno lahko dosežemo občutne prihranke v višini prevoženih km in s tem povezanih stroškov.
Dnevni prihranek pri kilometrih in s tem povezanih stroških bi bil zelo občuten, če bi vpeljali za vozila optimirane poti in optimirane vozne rede. To je tudi razumljivo, saj so sedanje poti dokaj neoptimirane, neracionalne in včasih po nepotrebnem podvajane, obremenitev voznega parka pa je pogostokrat preslabo izkoriščena.
7 Sklep
V prispevku so predstavljeni rezultati določitve optimalnih poti in optimalnih voznih redov vozil za potrebe razvoza otrok v šole, ki so izpeljani na osnovi izračunanih optimalnih postajališč.
Oboji optimalni rezultati, tako za postaje kot za poti in vozne rede, so izračunani v okviru dvokoračnega optimizacijskega postopka z namenom krčenja stroškov prevoza otrok v šole na območju občine Laško.
Za potrebe določitve optimalnih postaj je bila v 1. koraku uporabljena optimizacijska procedura, ki temelji na simulaciji Monte Carlo. Za to proceduro se predpostavlja, da doseže kar najmanjše možno število izračunanih optimalnih postaj, pri čemer le-te pokrivajo največje možno število učencev znotraj predpisanega radija. Slednjim je v povprečju potrebno hoditi najkrajše možne razdalje do postaj, hkrati pa je najmanjše možno tudi število nerazporejenih učencev.
Iz doseženih rezultatov je razvidno, da je možno določiti takšne pozicije 48 optimalnih postaj, ki bodo zmožne pokriti 554 od 562 učencev znotraj predpisanega radija pešačenja. Samo 8 učencev ostane nerazporejenih, vendar tudi njim ne bo potrebno prehoditi več kot nekaj 100 metrov daljše razdalje glede na ostalih 554 učencev.
V 2. koraku optimizacijskega postopka je potrebno glede na izračunane optimalne lokacije postaj iz prvega koraka izvesti še optimizacijo voznih poti in voznih redov prevoznih sredstev. V ta namen je bila uporabljena programska oprema, ki temelji na uporabi programov ArcLogistics in ArcView 9.31. V prispevku je podrobneje opisana metodologija za pripravo te opreme, ki vključuje zlasti naslednje nastavitve: osnovne nastavitve cestnega omrežja, specifikacijo vseh časovnih omejitev tako za transport od postaj do šol kot za obraten transport, specifikacijo voznega parka in stroškov vozil ter določitev vseh lokacij (izhodiščnih lokacij vozil, lokacij šol in optimalnih postaj).
Po opravljenih nastavitvah programske opreme se je izvedla optimizacija, ki je izračunala optimalne poti in vozne rede vozil za obe smeri transporta, od postaj do šol in obratne. Pri optimizaciji se je poskušalo doseči karseda minimalno število skupnih prevoženih kilometrov vozil, čim večjo napolnjenost vozil ter čim manj podvajanj poti.
Optimalne poti in vozni redi so se izračunali za vseh 14 vozil voznega parka, ki je na voljo občini Laško in obsega: 10 kombijev, 3 avtobuse ter 1 minibus. Kot kažejo doseženi rezultati, bi se dalo z dosledno uporabo optimalnih poti in voznih redov vozil občutno zmanjšati obstoječe stroške, do katerih prihaja v sedanjem stanju prevoza otrok v šolo. To pomeni zmanjšanje celo za 1.000 ali več km na dan, kar je vsekakor velik prihranek, ki bi se ga dalo doseči.
Doseženi rezultati za optimalne postaje, optimalne poti in vozne rede so bili predani naročniku, občini Laško. Pričakovati je, da se bodo z implementacijo teh rezultatov dosegli občutni dnevni prihranki pri prevozu otrok v šolo.
8 Literatura in viri
[1] Arends, B. (2003). Driving Delivery Productivity Using ArcLogistics Route and ArcView Tracking Analyst, Proceedings of the Twenty-Third Annual ESRI User Conference, San Diego.
[2] Bowerman, R., Calamai, H. B. (1995). A multiobjective optimization approach to urban school bus routing – formulation and solution method, Transportation Research part A – policy and practice, 29, 2, 107–123.
[4] Church, R. L., ReVelle, C. (1974). The maximal covering location problem, Papers of the regional science association, 32: 101–118.
[3] Dragan, D., Kramberger, T. (2009). Simulacijski pristop za potrebe določitve optimalnih avtobusnih postajališč v občini Laško. Embalaža, okolje, logistika, nov. 2009, št. 46, str. 42–45. [COBISS.SI-ID 512169789]
[4] Dragan, D., Kramberger, T. (2009). Simulation-Based Approach For the Purpose of Optimal Bus Stops Determination in Commune Lasko, Proceedings of the 6th International Conference on Logistic & Sustainable Transport 2009, Fakulteta za logistiko, Celje.
[5] ESRI (2000). Using Arclogistics Route, ESRI, Redlands, CA, USA.
[6] ESRI (2005). ESRI K–12 Solutions: School Bus Routing – Using ESRI Tools to Address the Problems, An ESRI White Paper, ESRI, Redands, California, USA.
[7] Gleason, J. M. (1975). A set covering approach to bus stop location, Elsevier, Omega, 3 (5): 605–608.
[8] Harmon, J. E., Anderson, S. J. (2003). The Design and Implementation of Geographic Information System, John Wiley & Sons, NY.
[9] Prasertsri, P., Kilmer, R. L. (2003). Improving Vertical Coordination from Farm-To-Plant Using A Cooperative, 2003 American Agricultural Economics Association Meetings in Montreal, Canada.
[10] Terrey, K. (2008). Arclogistics, The routing and scheduling solution for fleet management, ESRI, Redlands, CA, USA.